Reducción de problemas de geometría

Para poder resolver cualquier problema de geometría, y en particular, de tangencias en la circunferencia tenemos que tener claras las siguientes propiedades:

1. Si una recta es tangente a una circunferencia, el radio en el punto de tangencia es perpendicular a la tangente.

2. El centro de cualquier circunferencia que pase por dos puntos A y B, está en la mediatriz del segmento AB. Todo radio perpendicular a una cuerda la divide en dos partes iguales.

3. Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros.

4. El centro de cualquier circunferencia tangente a dos rectas r y s se encuentra en la bisectriz del ángulo que lo forman.

Pero...¿por que?

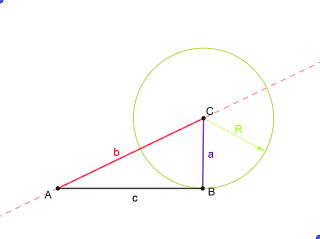
Todo empezó con nuestro gran amigo Pitágoras ( b²=a²+c² ) y su colaboración con el gran Thales y sus triángulos semejantes.

La recta que pasa por los puntos A y B es la tangente a la circunferencia, y la recta a, igual al radio.

La altura de un triángulo rectángulo es la media proporcional entre los dos segmentos en que divide a la base.

b/a = c/h = a/n

c/b = m/c = a/n

a/c = h/m = n/h

h² = m * n

Lo que nos lleva al concepto de Potencia; la potencia de un punto respecto a una circunferencia es el producto de la menos por la mayor distancia

 

Wp = b² = AD * AE

Wp = AH²

Ahora, con estos fundamentales, vamos a ver un ejemplo de cómo dos problemas aparentemente diferentes, encuentran una misma estrategia a la hora de trazar las circunferencias tangentes:

Ej 1: Circunferencia tangente a dos rectas (r y s) y un punto D.

Ej 2: Circunferencia tangente a dos puntos (P1 y P2) y a la recta t.

Como vemos en ambos ejercicios, la manera de solucionar el problema es el mismo, los datos de inicio varían pero, no Pitágoras, Thales y el concepto de Potencia, resultando sus propiedades de tangencias comunes. Podemos encontrar el camino siguiendo el mismo proceso.

Donde, comparando ambas figuras, vemos que los lugares geométricos coinciden conceptualmente, como ocurre con D=P1, G=P2, C=C, K=K1, J=K2, etc...y así sucesivamente.

Buena semana solventando problemas!!!