El Baricentro, ese gran desconocido

Baricentro, el punto que equilibra todo el triángulo.

Según la Real Academia Española (RAE), la palabra baricentro proviene del griego (βαρύς, barýs, "pesado, grave", y centro). En términos de física, se define como centro de gravedad, en geometría, como punto de intersección de las medianas de un triángulo.

Si profundizamos más allá de la propia definición de la RAE, nos encontraremos con que,

en geometría, el baricentro o , también llamado centroide, de una superficie contenida en una figura geométrica plana es un punto tal que cualquier recta que pasa por él divide a dicho segmento en dos partes de igual momento respecto a dicha recta. 

Se nombra como Ba.

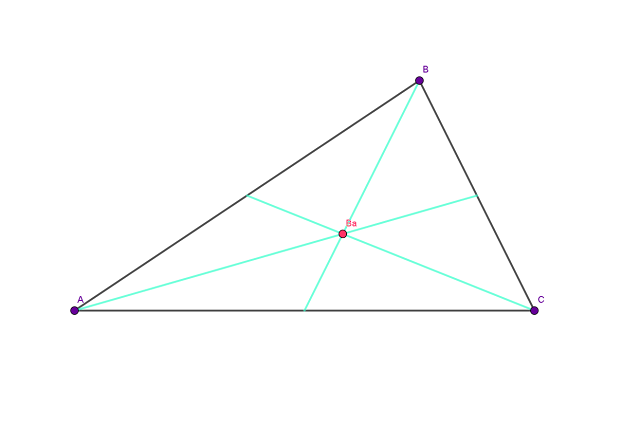Ba.Baricentro

Esto, básicamente, lo que nos viene a decir es que el baricentro, es el único punto en el que se cortan las 3 medianas de un triángulo.

Pero, ¿Qué es una mediana?

Una mediana de un triángulo es una recta que une un vértice del triángulo con el punto medio del lado opuesto a dicho vértice. También se puede definir la mediana como el segmento que une cada vértice con el punto medio del lado opuesto. 

Mb.Punto medio

Mediana

Ahora bien, ¿Cómo se calcula geométricamente el baricentro de un triángulo? 

1º. Localizamos el vértice B del triángulo.

2º. Calculas el punto medio del lado AC (lado opuesto al vértice B)

3º. Trazas la recta que pasa por el vértice B y el punto medio del lado AC. (Mediana)

4º. Se repite el mismo proceso con los vértices A y C

El punto en el que se cortan las 3 medianas, es el Baricentro.

Ba.Baricentro

Además, se cumple que el baricentro divide a cada mediana en dos segmentos, el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.

BBa.= 2BaMb ó  2k=j

Por último, y, profundizando también en la definición de la RAE, en física, el baricentro de un cuerpo material coincide con el centro de masas del mismo cuando el cuerpo es homogéneo (densidad uniforme) o cuando la distribución d

e materia en el cuerpo tiene ciertas propiedades, tales como la simetría.

¡Que paséis una buena semana!